
El valor de π se ha obtenido con diversas
aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el
número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclidianas.
El nombre π

Letra griega pi. Símbolo adoptado en
1706 por William Jones y popularizado por
Leonhard Euler.
La notación con la
letra griega π proviene de la inicial de las palabras de origen
griegoπεριφέρεια 'periferia' y περίμετρον 'perímetro' de un
círculo,
1 notación que fue utilizada primero por
William Oughtred (1574-1660) y cuyo uso fue propuesto por el matemático galés
William Jones2 (1675-1749); aunque fue el matemático
Leonhard Euler, con su obra
Introducción al cálculo infinitesimal, de
1748, quien la popularizó. Fue conocida anteriormente como
constante de Ludolph (en honor al matemático
Ludolph van Ceulen) o como
constante de Arquímedes (que no se debe confundir con el
número de Arquímedes). Jones plantea el nombre y símbolo de este número en 1706 y Euler empieza a difundirlo en 1736.
3
Arquímedes lo calculó con la aproximación de

< π <

, tal como consignó en su obra
Medición del círculo, ciertamente con otra notación.
4
Historia del cálculo del valor π
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.
Antiguo Egipto
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año
1800 a. C., descrito en el
papiro Rhind,
5 donde se emplea un valor aproximado de π afirmando que el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9; es decir, igual a 8/9 del diámetro. En notación moderna:


Entre los ocho documentos matemáticos hallados de la
antigua cultura egipcia, en dos se habla de
círculos. Uno es el
papiro Rhind y el otro es el
papiro de Moscú. Sólo en el primero se habla del valor aproximado del número π. El investigador
Otto Neugebauer, en un anexo de su libro
The Exact Sciences in Antiquity,
6 describe un método inspirado en los problemas del papiro de Ahmes para averiguar el valor de π, mediante la aproximación del área de un cuadrado de lado 8, a la de un círculo de diámetro 8.
Mesopotamia
Referencias bíblicas
Una de las referencias indirectas más antiguas del valor aproximado de π se puede encontrar en un versículo de la
Biblia:
«Hizo fundir asimismo un mar de diez
codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos».
«También hizo un mar de metal fundido, el cual tenía diez codos de un borde al otro, enteramente redondo; su altura era de cinco codos, y un cordón de treinta codos de largo lo ceñía alrededor».
Ambas citas dan 3 como valor de π lo que supone una notable pérdida de precisión respecto de las anteriores estimaciones egipcia y mesopotámica.

Método de
Arquímedes para encontrar dos valores que se aproximen al número
π, por exceso y defecto.
Abreviando el articulo de la web, pasamos a ver:
Fórmulas que contienen el número π
En geometría
- Área del círculo de radio r: A = π r²
- Área interior de la elipse con semiejes a y b: A = π ab
Áreas de cuerpos de revolución:
Volúmenes de cuerpos de revolución:
- Volumen de la esfera de radio r: V = (4/3) π r³
- Volumen de un cilindro recto de radio r y altura h: V = π r² h
- Volumen de un cono recto de radio r y altura h: V = π r² h / 3
- Ángulos: 180 grados son equivalentes a π radianes.
- El volumen del toro conlleva π al cuadrado24
En cálculo
- Área limitada por la astroide: (3/8) π a225
- Área de la región comprendida por el eje X y un arco de la cicloide: 3 π a2
- Área encerrada por la cardioide: (3/2) π a2
- Área de la región entre el eje polar y las dos primeras vueltas de la espiral de Arquímedes r = aα26 es 8π3 a2
- Área entre la curva de Agnesi y la asíntota es S = πa2.27
- Cisoide
- Estrofoide
- Caracol de Pascal. El área usando esta curva y cualquiera de las anteriores lleva en la fórmula el valor de pi28
En probabilidad
- La probabilidad de que dos enteros positivos escogidos al azar sean primos entre sí es: 6/π²
- Si se eligen al azar dos números positivos menores que 1, la probabilidad de que junto con el número 1 puedan ser los lados de untriángulo obtusángulo es: (π-2)/4
- El número medio de formas de escribir un entero positivo como suma de dos cuadrados perfectos es π/4 (el orden es relevante).
- Aguja de Buffon: si lanzamos al azar una aguja de longitud L sobre una superficie en la que hay dibujadas líneas paralelas separadas una distancia D, la probabilidad de que la aguja corte a una línea es: 2L/Dπ
En análisis matemático
-

- También como desarrollo en series:

- Formas de representación aproximada a
 29
29

![\sqrt[29] {261424513284461} \approx \pi](https://upload.wikimedia.org/math/6/f/3/6f386855bd170a26644f048d61d59400.png)
- Método de Montecarlo
- En un círculo de radio r inscrito en un cuadrado de lado 2r (2 veces el radio), el área del círculo es πr² y la del cuadrado (2r)². De esto se deduce que la relación de área entre el cuadrado y el círculo de π/4.30
- Fórmula de Srinivāsa Rāmānujan demostrada en 1985 por Jonathan y Peter Borwein, descubierta en 1910. Es muy eficaz porque aporta 8 decimales a cada iteración:
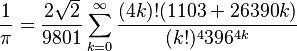
Cómputos de π
Pi y los números primos

donde
pn es el
n-ésimo número primo.
Euler fue el primero en hallar este valor de la función zeta (empleando la expresión de sumatoria) y resolviendo así el famoso
Problema de Basilea.
Fórmula de Machin
Una forma exacta de poder calcular π en términos de tangentes inversas de fracciones unitarias es la
fórmula de Machin, descubierta en
1706:
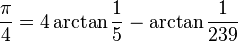
Muchos matemáticos emplearon esta fórmula para averiguar dígitos por encima de la centena (por ejemplo, el ya citado Shanks, que con esta fórmula calculó 707 posiciones decimales de π).
Métodos eficientes
Los primeros millones de dígitos de
π y 1/
π se pueden consultar en
Proyecto Gutenberg (véase
enlaces externos). Uno de los récords más recientes fue alcanzado en diciembre de
2002 por
Yasumasa Kanada de la
Universidad de Tokio, fijando el número pi con 1.241.100.000.000 dígitos; se necesitaron unas 602 horas con un
superordenador de 64 nodos
Hitachi SR8000 con una memoria de un terabyte capaz de llevar a cabo 2 billones de operaciones por segundo, más de seis veces el record previo (206 mil millones de dígitos). Para ello se emplearon las siguientes fórmulas modificadas de Machin:
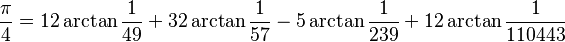

Estas aproximaciones proporcionaron una cantidad tan ingente de dígitos que puede decirse que ya no es útil sino para comprobar el funcionamiento de los superordenadores. La limitación no está en la computación sino en la memoria necesaria para almacenar una cadena con una cantidad tan grande de números.
Aproximaciones geométricas a π
Es posible obtener una aproximación al valor de π de forma geométrica. De hecho, ya los griegos intentaron obtener sin éxito una solución exacta al problema del valor de π mediante el empleo de
regla y compás. El problema griego conocido como
cuadratura del círculo o, lo que es lo mismo, obtener un cuadrado de área igual al área de un círculo cualquiera, lleva implícito el cálculo del valor exacto de π.
Una vez demostrado que era imposible la obtención de π mediante el uso de regla y compás, se desarrollaron varios métodos aproximados. Dos de las soluciones aproximadas más elegantes son las debidas a Kochanski (usando regla y compás) y la de
Mascheroni (empleando únicamente un compás).
Método de Kochanski
Se dibuja una circunferencia de radio R. Se inscribe el triángulo equilátero OEG. Se traza una recta paralela al segmento EG que pase por A, prolongándola hasta que corte al segmento OE, obteniendo D. Desde el punto D y sobre ese segmento se transporta 3 veces el radio de la circunferencia y se obtiene el punto C. El segmento BC es aproximadamente la mitad de la longitud de la circunferencia.
- Demostración (suponiendo R = 1)
Sustituyendo en la primera fórmula:
Método de Mascheroni
Método desarrollado por
Lorenzo Mascheroni: se dibuja una circunferencia de radio R y se inscribe un hexágono regular. El punto D es la intersección de dos arcos de circunferencia: BD con centro en A', y CD con centro en A. Obtenemos el punto E como intersección del arco DE, con centro en B, y la circunferencia. El segmento AE es un cuarto de la longitud de la circunferencia, aproximadamente.
- Demostración (suponiendo R = 1)
Por el teorema de Ptolomeo, en el cuadrilátero ABEB'
Uso en matemática y ciencia
π es ubicuo en matemática; aparece incluso en lugares que carecen de una conexión directa con los círculos de la geometría euclídea.
31
Geometría y trigonometría
Para cualquier
círculo de radio
r y diámetro
d = 2
r, la longitud de la
circunferencia es π
d y el área del círculo es π
r2. Además, π aparece en fórmulas para áreas y volúmenes de muchas otras figuras geométricas relacionadas con la circunferencia, como
elipses,
esferas,
conos, y
toroides.
32 π aparece en
integrales definidas que describen la circunferencia, área o volumen de figuras generadas por circunferencias y círculos. En el caso básico, la mitad del área de un
círculo unitario es:
33
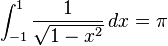
De la definición de las
funciones trigonométricas desde el círculo unitario se llega a que el seno y el coseno tienen período 2π. Lo que significa, para todo
x y enteros
n, sin(
x) = sin(
x + 2π
n) y cos(
x) = cos(
x + 2π
n). Porque sin(0) = 0, sin(2π
n) = 0 para todos los enteros
n. Además, el ángulo 180° es igual a π radianes. En otras palabras 1° = (π/180) radianes.
En la matemática moderna, π es a menudo
definido usando funciones trigonométricas, por ejemplo como el menor entero positivo
x para el cual sin
x = 0, para evitar dependencias innecesarias de las sutilezas de la geometría euclidiana y la integración. Equivalentemente, π puede ser definido usando funciones trigonométricas inversas, por ejemplo como π = 2 arccos(0) o π = 4 arctan(1). Expandir funciones trigonométricas inversas como
series de potencias es la manera más fácil de obtener series infinitas para π.
Variable compleja


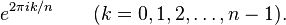
Cálculo superior
 37
37
Una consecuencia es que el resultado de la
división entre la
función gamma de un semientero (la mitad de un número impar) y √π es un número racional.
Física
Aunque no es una
constante física,
π aparece rutinariamente en ecuaciones que describen los principios fundamentales del Universo, Debido en gran parte a su relación con la naturaleza del círculo y, correspondientemente, con el
sistema de coordenadas esféricas. Usando unidades como las
unidades de Planck se puede eliminar a veces a
π de las fórmulas.
Probabilidad y estadística


Nótese que para todas las funciones de densidad de probabilidad se cumple que
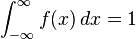
, entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para
π.
45

Representación del
experimentoen el modelo de la "aguja de Buffon", se lanzan dos agujas (
a,
b) ambas con longitud
l. En el dibujo la aguja
aestá cruzando la línea mientras que la aguja
b no.
El problema de la
aguja de Buffon es llamado en ocasiones como una aproximación empírica de
π. Se trata de lanzar una aguja de longitud
l repetidamente sobre una superficie en la que se han trazado rectas paralelas distanciadas entre sí, en
t unidades, de manera uniforme (con
t >
l de forma que la aguja no pueda tocar dos rectas). Si la aguja se lanza
n veces y
x de esas cae cruzando una línea, entonces se puede aproximar
π usando el
Método de Montecarlo, lanzándola gran cantidad de veces:
46 47 48 49
Aunque este resultado es matemáticamente impecable, no puede usarse más que para determinar unos cuantos dígitos de
π experimentalmente. Para conseguirse sólo tres dígitos correctos (incluyendo el "3" inicial) requiere de millones de lanzamientos,
46 y el número de lanzamientos crece
exponencialmente con el número de dígitos deseados. Además, cualquier error en la medida de las longitudes
l y
t se transfiere directamente como un error en la aproximación de
π. Por ejemplo, una diferencia de un simple
átomo en una aguja de 10 centímetros podría acarrear errores en el noveno dígito del resultado. En la práctica, incertidumbres en la determinación de si la aguja en realidad cruza una línea que parece estar solo tocándola lleva el límite de precisión alcanzable a mucho menos de 9 dígitos.
Curiosidades
Aparición en medios
- En el año 1998 aparece una película del director Darren Aronofsky denominada Pi sobre un matemático que cree que el mundo se representa por números.
- Alfred Hitchcock en su film Cortina rasgada hace aparecer el símbolo π como una organización de espionaje.
- En la serie de dibujos The Simpsons, en el episodio "Bye Bye Nerdie", el Professor Frink grita, a voz en cuello, que "¡π es tres exactamente!", para atraer la atención de un auditorio compuesto por científicos. Cuando todos se dan vuelta para mirarlo, pide disculpas por haberse visto obligado a semejante sacrilegio.
- La novela Contacto de Carl Sagan —sobre la que luego se filmó la película homónima— toma a π (aunque no en base decimal) como un número que esconde la esencia misma del universo.

"Piso-Pi",
mosaico en la entrada del edificio de la matemática en TU
Berlín.

Detalle del "Mazda Pi", se añadieron 27 cifras decimales de π a este automóvil.
- 355/113 (~3.1415929) se menciona a veces como una simulación ¡cuasi-perfecta!
- El primer millón de cifras de π y su inversa 1/π se puede consultar en el Proyecto Gutenberg o en este enlace.
- Se emplea este número en la serie de señales enviadas por la tierra con el objeto de ser identificados por una civilización inteligente extraterrestre.
- La probabilidad de que dos enteros positivos escogidos al azar sean primos entre si es
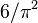 .
.
- En algunos lenguajes de programación se pueden averiguar tantos dígitos como se desee con simplemente emplear expresiones como: RealDigits[ N[ Pi, 105]] en «Mathematica».
- El 4 de octubre de 2006, a la 1:30 de la madrugada, y tras 16 horas y media, el japonés Akira Haraguchi volvió a romper su propio record recitando 100.000 dígitos del número pi, realizando una parada cada dos horas de 10 minutos para tomar aire.
- Existe una canción de Kate Bush llamada "Pi" en la cual se recitan más de veinte dígitos decimales del número.
- En Argentina, el número telefónico móvil para emergencias en estaciones de trenes y subterráneos es ∗31416.
- El valor principal de la expresión
 es un número real y está dado por55
es un número real y está dado por55

- Srinivasa Ramanujan publicó una solución aproximada, con regla y compás, a la cuadratura del círculo en 1913 en la que obtuvo un segmento aproximadamente igual a
 :57
:57

- Los hebreos consideran al número pi como "el número de Dios". En la película Pi: Fe en el Caos los estudiantes de la Torá consideran los 216 (6x6x6) primeros decimales como representación del verdadero nombre de Dios. En la Biblia (hebrea y cristiana) el nombre de Dios aparece en el capítulo 3 y versículo 14 del Libro del Éxodo (Éxodo 3,14).
Cuestiones abiertas sobre π
- Cada uno de los dígitos decimales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, ¿tiene una aparición infinita en los decimales de π?
- La denominada cuestión de Brouwer: en la expansión decimal de π, ¿existe alguna posición donde exista una sucesión de mil ceros consecutivos?
- ¿Es π simplemente normal en base 10? Es decir, ¿tiene cada uno de los diez dígitos del sistema decimal la misma probabilidad de aparición en una expansión decimal?
- No se sabe si π+e, π/e, ln(π) son irracionales. Se sabe que no son raíces de polinomios de grado inferior a nueve y con coeficientes enteros del orden 109.58 59
Véase también
Referencias
- Volver arriba↑ G L Cohen and A G Shannon, John Ward's method for the calculation of pi, Historia Mathematica 8 (2) (1981), 133-144
- Volver arriba↑ New Introduction to Mathematics, William Jones, 1706, London
- Volver arriba↑ Beskin. "Fracciones maravillosas" Mir Moscú, (1987)
- Volver arriba↑ Beskin: "Fracciones maravillosas", Editorial Mir, Moscú, (1987)
- Volver arriba↑ Gay Robins y Charles Shute: The Rhind Mathematical Papyrus: an ancient Egyptian text, British Museum Publications, London, 1987, véase “Squaring the Circle”, páginas 44 a 46.
- Volver arriba↑ "The Exact Sciences in Antiquity", Otto Neugebauer, 1957, Dover, New York,(nueva edición de 1969).
- Volver arriba↑ Petr Beckmann: A History of Pi, publicado por primera vez por The Golem Press, 1971, edición consultada por Barnes and Books, New York, 1993.



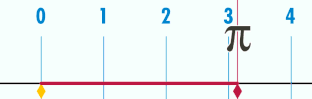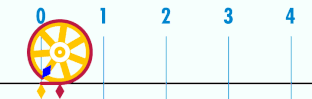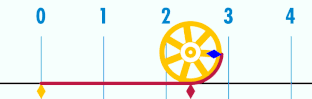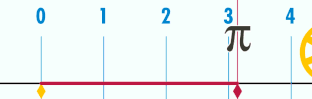
 es la relación entre la longitud de una
es la relación entre la longitud de una 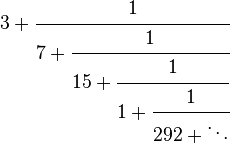

 < π <
< π <  , tal como consignó en su obra Medición del círculo, ciertamente con otra notación.
, tal como consignó en su obra Medición del círculo, ciertamente con otra notación.







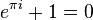
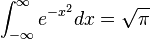






![\sqrt[29] {261424513284461} \approx \pi](https://upload.wikimedia.org/math/6/f/3/6f386855bd170a26644f048d61d59400.png)
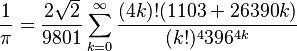

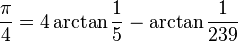
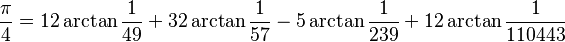














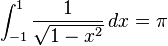


 y e ≈ 2.71828 es
y e ≈ 2.71828 es 
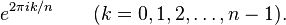



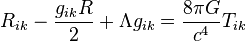





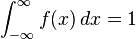 , entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.
, entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.





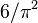 .
. es un número real y está dado por
es un número real y está dado por
 :
: